I had my elementary ed class canceled for low enrollment this fall. Make of that what you will.
The replacement course is College Algebra. Ironically named, since it is mostly Algebra 2. Which is required in Michigan. Our sequence has been 097 (prealgebra) -> 110 intermediate algebra (algebra 1) -> 122 College Algebra. It used to be + 123 (trigonometry) to go on to Calculus, but we have a nice precalc class now (124) so people needing to take calculus that don't place into it can just take 1 semester. The audience for 122 then, is now general education, and people who need courses that require it, like the basic chemistry, intro physics, and statistics. It's a 3 credit course, and my section meets twice a week.
The course has traditionally been quadratics -> polynomials -> rational functions -> exponentials -> logarithms -> light touch of statistics. So what do we want from the quadratics unit? This post is me trying to think out loud to get it straight for myself. The schedule is pretty packed, so I have 2-3 weeks per topic, 4-6 class periods.
The instructional sequence I have planned is visual patterns -> modeling (Penny Circle and Will It Hit the Hoop?) -> graphing/equation forms (Match My Parabola & Form Fix) -> solving equations (vertex form & graphing), mostly in a modeling context.

The visual patterns do a lot of work. They offer a hook, they give learners a chance to notice and wonder, they give us a chance to problem solve. They are also different from what most students have seen in algebra, sadly, so offer a way to let them know that this course might be different. I also have them read Elizabeth Statmore's post on math as a thinking class. I asked them, "What do you think the main idea is? How does this compare with your own ideas about learning math or your previous experiences?" and you can read their responses on this doc. I think they get it. Mathematically, I think my main point is the use of variable as a relationship rather than an unknown. The transition from step number to x is very natural. Secondarily, they get to see multiple equivalent expressions. Which is one of those math ideas which many learners see as a bug, but mathematicians think is a central feature. Part of the richness of these problems is what the old NCTM standards called the representation process standard. Tables, expressions, visual and the connections between them all move us forward. Here's a handout with four quadratic patterns. The bricks and the darts and kites are very difficult to visual make a symbolic rule for. I might have made them or might have found them at Fawn Nguyen's visualpatterns.org or it could be a mix.
Modeling is a key theme of the course, and Penny Circle and Will It the Hoop? are a good start to it. I was surprised how many learners went with an exponential form, and the reveal is the perfect way to settle it. We will be using Desmos activities a lot, and those are pretty slick introductions. The Penny Circle builds on the covariation use of variables, and the basketball leads into the graphing we'll be working on next.
This is where we are as I write.
I'm convinced that one of the barriers for these students is understanding graphs. Thankfully, making them is easier than ever. But I don't think that many know how to think with them. Again with the representation standard, the connections between the symbolic expression and the graph is mostly taxonomical, and I want it to have meaning. Though this is a place where I could use some help. Regression supports this goal, as it brings tables into the web of connections. Activities where they vary parameteers and observe the effect on the graph help, at least in terms of taxonomy. Solving equations with graphs is an opportunity to build some of the understanding I want, as, especially for applications, the context is another piece of the representation. Writing this, I'm a little surprised by how hard it is for me to put my goal here into words. That would undoubtedly help with the teaching!Solving equations is last for me, partly because it is so much what they perceived the focus to be in their previous math courses. I don't care especially for a lot of symbolic skill here. I don't teach solving by factoring, though the factored form in connection with graphs is something I emphasize. I do like the approach of solving from quadratic form, because it builds on a theme in math I love about doing and undoing. This leads better into exponentials and logarithms than it does polynomials and rational functions. The symbolic fluency that I want is being able to see a quadratic as series of steps. Take a number, subtract 2, square it, double it, add five is the same as 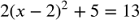 . To find what numbers make 13 from that function, we can do by undoing. I love Graspable Math for this, as the dragging to undo seems to really help get across the idea, though it doesn't work on the balance nature of equations. Here's an example GM activity with 3 quadratics to solve.
. To find what numbers make 13 from that function, we can do by undoing. I love Graspable Math for this, as the dragging to undo seems to really help get across the idea, though it doesn't work on the balance nature of equations. Here's an example GM activity with 3 quadratics to solve.
I'm very interested in your thoughts. What are the key ideas you want in a quadratics unit? What am I leaving out that you love? What understanding do you want your learners to develop or skills do you want them to have for graphing? Why?
P.S.
Probably violating some internet rule here, but really liking the Twitter discussion about this post.
@DavidKButlerUoA: This line was very interesting: "multiple equivalent expressions... is one of those math ideas which many learners see as a bug, but mathematicians think is a central feature". I'd love to hear more about that.
@joshuazucker: My interpretation is that beginners may want there to be only one answer and experts see how useful it is to have multiple representations that make different behaviors immediately visible.
@mathcurmudgeon: When 90% of calculus (and every math course, really) is rewriting expressions in an equivalent form that we can work with more easily.
@mathhombre: it starts with fractions. All these different ways to write the same thing. One of them must be right. (Often supported by teachers insisting on one.) But that we can transform, rewrite and tinker leads to fluency, connections, and meaning.
@mathforge: The belief that out of all the ways of writing it there must be a RIGHT way is SUCH an interesting belief. I've never thought before that people might believe this.
I suspect that this is more prevelant than we might admit. As experienced mathematicians we might chuckle at people who think that there is a "best" way to write, say, a quadratic or a fraction. But we probably fall into the same trap with ideas.
I might, to take a random example, think that there is a "right" way to think about differentiation, or Pythagoras theorem, or a topology, or the category of smooth functions. What I mean is, "this is the way I find most intuitive".
===
@KarenCampe: Love the visual patterns start & modeling focus.
When you do graphing equation forms & use match my graph/form fix you will surely cover symmetry of the graphs & how factoring gives x-ints. I like how graphing & alg manipulation of quadratics are interconnected...
Use graphing as tool to support any algebraic rearranging we might want. Look for hidden parabola that shows complex roots. Axis of symm hidden in quadratic formula.
===
[In response to "Quadratics unit in a college algebra course. What goes in, what's left out? "]
@theresawills: Probably too vague, but worth saying: RICH PROBLEM SOLVING.



























