While Math Hombre is traditionally ad free, I do owe a link to my daughter Ysabela. In exchange for her review of Babymouse: Dragonslayer, the excellent math/fantasy graphic novel by Jennifer Holm, I promised to plug her market craft.
Yzzy's Sticky Silverware has recycled silverware affixed with two powerful magnets and artistic embellishments to make a beautiful and practical refrigerator decoration. A steal at $1.25 decorated ($1 plain), you might pay up to $5 for a similar product at a craft show. Check it out! Mailing is at cost.
Some of the math involved was: figuring out the unit cost from the total materials cost, and also balances, profit margin, the length of the total wire based on the wire per silverware, (which was a pretty good upper el measurement problem). What is her break even point? That's the next calculation!
Thursday, October 29, 2009
Sunday, October 25, 2009
Area Block
New game! Blokus meets Nim, this game works on area and strategy. Tested with fourth and fifth graders, but flexible upwards with sophistication in area computation techniques. Get it as a pdf here: AreaBlock.pdf
Materials: Game Board, 2 different color pens, pencils, crayons or markers.
How to play: Players take turns making a single shape on the board that has an area of 10 or less. The game is done when the board is filled, and the player with the most squares covered wins. The table is for recording how many squares you cover each turn.
The first player to go can only color up to 8 squares on their first shape. (Otherwise it would always be best to go first.) After that the limit is always 10.
The squares colored in to make your shape need to share a side, not just touch at a corner. (The shape you make has to be a polygon.) A player can even use slanted lines – as long as they can figure out the area for their shape! When you are making a new shape, it does not have to touch your old – you can put it anywhere there’s room.
After you make or shade in your shape, record the area of your block – you don’t want to miss any points. The next player then colors a polygon of up to 10 squares of area in a different color.
When the board is completely filled, the game is done. Total up your squares and see who won!
Notice you can check if all the squares are counted by adding both scores – you should get 100.
Whoever lost gets to choose the next time if they want to go first or second.
Variations:
• The board can be changed to have holes or blocks or be a different shape. As long as there are 100 squares. After trying these boards, make your own.
• The game can be played with dice. Roll 2 dice, and you can fill in the total rolled.
• Advanced players could try where their score is not the area – but the perimeter. (You might want to try that with no slanted sides.)
Board 0:
Board 1:
Board 2:
Board 3:
Board 4:
It's pretty fun! I haven't been able to spot a degenerate strategy yet. Give it a try, and let me know what you think.
Materials: Game Board, 2 different color pens, pencils, crayons or markers.
How to play: Players take turns making a single shape on the board that has an area of 10 or less. The game is done when the board is filled, and the player with the most squares covered wins. The table is for recording how many squares you cover each turn.
The first player to go can only color up to 8 squares on their first shape. (Otherwise it would always be best to go first.) After that the limit is always 10.
The squares colored in to make your shape need to share a side, not just touch at a corner. (The shape you make has to be a polygon.) A player can even use slanted lines – as long as they can figure out the area for their shape! When you are making a new shape, it does not have to touch your old – you can put it anywhere there’s room.
After you make or shade in your shape, record the area of your block – you don’t want to miss any points. The next player then colors a polygon of up to 10 squares of area in a different color.
When the board is completely filled, the game is done. Total up your squares and see who won!
Notice you can check if all the squares are counted by adding both scores – you should get 100.
Whoever lost gets to choose the next time if they want to go first or second.
Variations:
• The board can be changed to have holes or blocks or be a different shape. As long as there are 100 squares. After trying these boards, make your own.
• The game can be played with dice. Roll 2 dice, and you can fill in the total rolled.
• Advanced players could try where their score is not the area – but the perimeter. (You might want to try that with no slanted sides.)
Board 0:
Board 1:
Board 2:
Board 3:
Board 4:
It's pretty fun! I haven't been able to spot a degenerate strategy yet. Give it a try, and let me know what you think.
Tuesday, October 13, 2009
GeoGebra: Triangle Tuning
What can we deduce from the side lengths of a triangle?
This is a preservice teacher activity, easily adaptable to middle or high school use. GeoGebra is a free dynamic geometry program available as an online applet or downloadable program, from geogebra.org.
Objective: TLW explore triangle properties relating type and side length.
Schema Activation: What are the 7 triangle types? Fill them in in the ‘Type’ column below. You'll fill in the other columns as you go through the activity.
.....Type ....................... Examples [Like (3,5,5) ] .......................What do you notice?
1.
2.
3.
4.
5.
6.
7.
Focus: One of the reasons dynamic geometry is so powerful is the support it allows the teacher (or curriculum designer) to give students for finding examples. Lots of examples. As we’ve discussed in class, the natural way we reason is to go from lots of specific examples to the general.
Activity:
1) Open the sketch TriangleBySide.ggb. (Online at faculty.gvsu.edu/goldenj/TriangleBySide.html)
a. Collect at least 2 examples of each type of triangle. Where possible, try not to have the triangles be similar, where all the sides are multiples of another triangle.
b. Which were hardest to find? Was it something to do with the type or how you were looking?
2) Open the sketch PythagoreanData.ggb. (Online at faculty.gvsu.edu/goldenj/PythagoreanData.html)
a. Look at your right triangle examples on this triangle. How do you think ancient mathematicians noticed this cool pattern with the squares
b. Check your other examples on this sketch. For each, record whether the sum of the areas of the smaller squares is <, =, or > the area of the large square.
c. What pattern(s) do you notice?
d. Why do you think your pattern(s) might be true?
3) Go to http://teachers.henrico.k12.va.us/math/GeoGebra_Site/pythagoras/pythaPrblm1.html (link on Blackboard) for the Ladder sketch. Answer the questions there.
a. How high will he get if he places the ladder 3 m off the wall? Drag the ladder point and find a solution. Sketch the solution with all its lengths (s, r, h) on paper.
b. Now, calculate the solution of task (a) on paper. Which lengths are given, which are sought? Do you get the same solution?
c. At what distance of the wall should Pythagoras place his ladder in order to reach the window 4.50 m above the ground? Sketch the solution with all its lengths (s, r, h) on paper.
d. Now, calculate the solution of task (c) on paper. Compare your solution to your sketch?
e. As a teacher, what do you notice about the difference between doing the tasks in sketch and on the paper?
4) Open the sketch AdjustableLadder.ggb (Online at faculty.gvsu.edu/goldenj/AdjustableLadder.html)
a. What young Pythagoras might not have known is that a safe ladder ratio is 4:1 for the height to distance from the wall. What length ladder does he need to reach the window safely? Is there one solution or more?
b. How would you solve this problem on paper?
Reflection:
a. What confirmed, new or deepened understanding did you develop regarding triangles through these activities?
b. How did the dynamic environment affect your understanding?
EDIT:
Be sure to look at the comments. Scott Farrar has some notes on using this with 9th grade geometry, and has added a complimentary activity.
This is a preservice teacher activity, easily adaptable to middle or high school use. GeoGebra is a free dynamic geometry program available as an online applet or downloadable program, from geogebra.org.
Objective: TLW explore triangle properties relating type and side length.
Schema Activation: What are the 7 triangle types? Fill them in in the ‘Type’ column below. You'll fill in the other columns as you go through the activity.
.....Type ....................... Examples [Like (3,5,5) ] .......................What do you notice?
1.
2.
3.
4.
5.
6.
7.
Focus: One of the reasons dynamic geometry is so powerful is the support it allows the teacher (or curriculum designer) to give students for finding examples. Lots of examples. As we’ve discussed in class, the natural way we reason is to go from lots of specific examples to the general.
Activity:
1) Open the sketch TriangleBySide.ggb. (Online at faculty.gvsu.edu/goldenj/TriangleBySide.html)
a. Collect at least 2 examples of each type of triangle. Where possible, try not to have the triangles be similar, where all the sides are multiples of another triangle.
b. Which were hardest to find? Was it something to do with the type or how you were looking?
2) Open the sketch PythagoreanData.ggb. (Online at faculty.gvsu.edu/goldenj/PythagoreanData.html)
a. Look at your right triangle examples on this triangle. How do you think ancient mathematicians noticed this cool pattern with the squares
b. Check your other examples on this sketch. For each, record whether the sum of the areas of the smaller squares is <, =, or > the area of the large square.
c. What pattern(s) do you notice?
d. Why do you think your pattern(s) might be true?
3) Go to http://teachers.henrico.k12.va.us/math/GeoGebra_Site/pythagoras/pythaPrblm1.html (link on Blackboard) for the Ladder sketch. Answer the questions there.
a. How high will he get if he places the ladder 3 m off the wall? Drag the ladder point and find a solution. Sketch the solution with all its lengths (s, r, h) on paper.
b. Now, calculate the solution of task (a) on paper. Which lengths are given, which are sought? Do you get the same solution?
c. At what distance of the wall should Pythagoras place his ladder in order to reach the window 4.50 m above the ground? Sketch the solution with all its lengths (s, r, h) on paper.
d. Now, calculate the solution of task (c) on paper. Compare your solution to your sketch?
e. As a teacher, what do you notice about the difference between doing the tasks in sketch and on the paper?
4) Open the sketch AdjustableLadder.ggb (Online at faculty.gvsu.edu/goldenj/AdjustableLadder.html)
a. What young Pythagoras might not have known is that a safe ladder ratio is 4:1 for the height to distance from the wall. What length ladder does he need to reach the window safely? Is there one solution or more?
b. How would you solve this problem on paper?
Reflection:
a. What confirmed, new or deepened understanding did you develop regarding triangles through these activities?
b. How did the dynamic environment affect your understanding?
EDIT:
Be sure to look at the comments. Scott Farrar has some notes on using this with 9th grade geometry, and has added a complimentary activity.
Math Resources
Moodle
Moodle Math documentation
http://docs.moodle.org/en/Mathematics
Pretty technical information, but accurate and detailed.
Book about teaching math with Moodle
http://www.packtpub.com/moodle-1-9-math/book
Content
http://illuminations.nctm.org/
NCTM’s free lesson and resource center, with many online applets. Note the Calculation Nation link leads to some excellent 1 and 2 player games, but require a free login account. (Guest access to try it.)
http://ohiorc.org/for/math/
An Ohio Resource Center with links to many topics by grade and content. Some high quality resources.
http://nrich.maths.org
From the British equivalent of the NCTM. Once you get past how they say ‘maths,’ there’s an excellent supply of interesting problems, some clever student solutions, and open challenges. Also features some interactive applets.
Internet Resources for in class use
http://math.hippocampus.org/
An extensive collection of online exposition of topics from algebra and calculus. (As well as Bio, Chemistry, Physics, etc. Some support for Spanish.) Includes a voice delivering reading of the text (with a skip forward feature), and assessment along the way. Not clear what the purchase of a license adds, but everything I’ve seen was free.
http://www.imagination3.com/
GE’s interactive whiteboard, open to collaboration, optional graph paper background. Colors and some shapes are possible. You can save files.
http://www.wolframalpha.com/
Wolfram|Alpha, a free computational engine online. Amazing and worth exploring. Also some encyclopedia function. Supercedes some of the older online utilities.
http://geogebra.org
GeoGebra, a free dynamic geometry program that can be used as a web app or by downloading and installing. Some powerful algebraic applications, too.
http://www.plu.edu/~heathdj/java/
A collection of java applets, from many different mathematical content areas.
http://www.univie.ac.at/future.media/moe/onlinewerkzeuge.html
Powerful collection of online tools. One of the best online function plotters (graphing calculator) is here.
Games
http://www.funbrain.com/brain/MathBrain/MathBrain.html
K-8 math games. Not very challenging, but there are students for wom this will be just right. Connected with Poptropica, which my kids love, and features some decent problem solving.
http://gprime.net/game/
Huge collection of flash games – not all kid appropriate. Some excellent math and reasoning games, though. Try 3D logic, a maze game on 3 cube faces (http://gprime.net/game.php/3dlogic), gridlock, the classic game (http://gprime.net/game.php/gridlock) or grow island, a deductive reasoning game (http://gprime.net/game.php/growisland), and one of a family of grow games (http://www.eyezmaze.com/grow/v3/index.html).
http://www.logicmazes.com/
Very challenging puzzles by a very interesting man, Robert Abbott. Also links to some games of his creation.
Utility
http://incompetech.com/graphpaper/lined/
Free graph paper pdf generator. Very handy.
Teacher
http://www.learner.org/resources/browse.html?discipline=5
Annenberg Teacher Resource Center. Extensive collection of lessons, videos of students and teachers, and professional development materials. All free. Sortable by grade level.
Moodle Math documentation
http://docs.moodle.org/en/Mathematics
Pretty technical information, but accurate and detailed.
Book about teaching math with Moodle
http://www.packtpub.com/moodle-1-9-math/book
Content
http://illuminations.nctm.org/
NCTM’s free lesson and resource center, with many online applets. Note the Calculation Nation link leads to some excellent 1 and 2 player games, but require a free login account. (Guest access to try it.)
http://ohiorc.org/for/math/
An Ohio Resource Center with links to many topics by grade and content. Some high quality resources.
http://nrich.maths.org
From the British equivalent of the NCTM. Once you get past how they say ‘maths,’ there’s an excellent supply of interesting problems, some clever student solutions, and open challenges. Also features some interactive applets.
Internet Resources for in class use
http://math.hippocampus.org/
An extensive collection of online exposition of topics from algebra and calculus. (As well as Bio, Chemistry, Physics, etc. Some support for Spanish.) Includes a voice delivering reading of the text (with a skip forward feature), and assessment along the way. Not clear what the purchase of a license adds, but everything I’ve seen was free.
http://www.imagination3.com/
GE’s interactive whiteboard, open to collaboration, optional graph paper background. Colors and some shapes are possible. You can save files.
http://www.wolframalpha.com/
Wolfram|Alpha, a free computational engine online. Amazing and worth exploring. Also some encyclopedia function. Supercedes some of the older online utilities.
http://geogebra.org
GeoGebra, a free dynamic geometry program that can be used as a web app or by downloading and installing. Some powerful algebraic applications, too.
http://www.plu.edu/~heathdj/java/
A collection of java applets, from many different mathematical content areas.
http://www.univie.ac.at/future.media/moe/onlinewerkzeuge.html
Powerful collection of online tools. One of the best online function plotters (graphing calculator) is here.
Games
http://www.funbrain.com/brain/MathBrain/MathBrain.html
K-8 math games. Not very challenging, but there are students for wom this will be just right. Connected with Poptropica, which my kids love, and features some decent problem solving.
http://gprime.net/game/
Huge collection of flash games – not all kid appropriate. Some excellent math and reasoning games, though. Try 3D logic, a maze game on 3 cube faces (http://gprime.net/game.php/3dlogic), gridlock, the classic game (http://gprime.net/game.php/gridlock) or grow island, a deductive reasoning game (http://gprime.net/game.php/growisland), and one of a family of grow games (http://www.eyezmaze.com/grow/v3/index.html).
http://www.logicmazes.com/
Very challenging puzzles by a very interesting man, Robert Abbott. Also links to some games of his creation.
Utility
http://incompetech.com/graphpaper/lined/
Free graph paper pdf generator. Very handy.
Teacher
http://www.learner.org/resources/browse.html?discipline=5
Annenberg Teacher Resource Center. Extensive collection of lessons, videos of students and teachers, and professional development materials. All free. Sortable by grade level.
Thursday, October 8, 2009
Money Problems
Excellent variation on the "how many ways to make change problem" at the New York Times today. The Freakonomics column is reporting the work of Patrick DeJarnette. I can see giving this problem from 4th grade to linear algebra!
Click on the money tag to see my previous money games. Click on the cartoon to go to the excellent Non Sequitur website.
Saturday, October 3, 2009
Math Teachers at Play #16
The new carnival is up.
A clock face activity for learning how to tell time supports students with a nice simple representation. The biographies reviewed here look like must buys. Very nice math teaching memoir from Math Mama. We should all write more of these. Denise, carnival originator, starts a good division discussion. Some interesting online math games are highlighted at the Innovative Educator.
The order of operations conversation reminded me of a student teacher I just saw who has picked up the nickname Aunt Sally. ("It's Not Funny," she said in response to my giggle.) I'm hugely in favor of a four step Order of Operations. It's also a great opportunity to discuss with students the difference between a result or theorem and a convention.
A clock face activity for learning how to tell time supports students with a nice simple representation. The biographies reviewed here look like must buys. Very nice math teaching memoir from Math Mama. We should all write more of these. Denise, carnival originator, starts a good division discussion. Some interesting online math games are highlighted at the Innovative Educator.
The order of operations conversation reminded me of a student teacher I just saw who has picked up the nickname Aunt Sally. ("It's Not Funny," she said in response to my giggle.) I'm hugely in favor of a four step Order of Operations. It's also a great opportunity to discuss with students the difference between a result or theorem and a convention.
Thursday, October 1, 2009
Anchor Charts
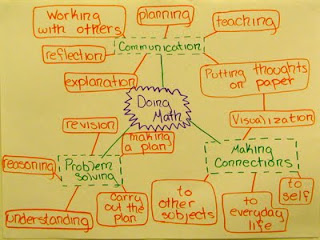
While we did this as a teacher prep activity, I think it would be interesting with K-12 students as well. I first heard about anchor charts in Mosaic of Thought (I think), and like how they serve as both assessment and culture building. I've had students make charts about a particular concept, about what to do when you're stuck, and for what it means to do, learn and teach mathematics.
For this most recent lesson I had the students read "Mind mapping As a Tool in Mathematics Education", by Astrid Brinkman from Mathematics Teacher, Feb 2003. (They had previously expressed curiosity about and a lack of experience with concept maps.) One reason I love these is that they are frequently surprising. I expect one like this, that echoes the NCTM process standards we emphasize in the first unit: (Remember you can click images to see them full size.)
But then they go and make these completely original things like:
 with different processes emphasized
with different processes emphasized
and
Instructions to the students:
Activity: Anchor Charts
The following example comes from Ellin Keene’s (2008) To Understand: "Teachers generate anchor charts to capture and celebrate increasing sophistication in oral language use." (p. 278)
If you substitute ‘understanding learning in mathematics’ for ‘oral language use,’ you have the purpose of this activity. (Follow a link for a free pdf of the first chapter, under samples.)
Create an Anchor Chart for Learning in Mathematics
1. Identify the concepts and ideas that you want to remember as they relate to doing mathematics.
2. Develop an anchor chart that captures and celebrates your increasing sophistication in understanding “Doing Mathematics.” This might be a list, or a mind map, or a representation of your own creation. You decide – just be prepared to share your chart during our next class.
3. Be sure you leave 10 minutes to reflect.
Reflection: How well does your group’s anchor chart capture what you want your future students to think of hen you ask them “what does it mean to do mathematics?”
Home Extension: You might want to check out how math teachers use anchor charts at books.google.com - Integrating Literacy and Math. by Ellen Fogelberg, Carole Skalinder, Patti Satz, Barbara Hiller, and Lisa Bernstein.
Other interesting examples:
Send me yours or your students' and I would be happy to post that!
For this most recent lesson I had the students read "Mind mapping As a Tool in Mathematics Education", by Astrid Brinkman from Mathematics Teacher, Feb 2003. (They had previously expressed curiosity about and a lack of experience with concept maps.) One reason I love these is that they are frequently surprising. I expect one like this, that echoes the NCTM process standards we emphasize in the first unit: (Remember you can click images to see them full size.)
But then they go and make these completely original things like:
 with different processes emphasized
with different processes emphasizedand
Activity: Anchor Charts
The following example comes from Ellin Keene’s (2008) To Understand: "Teachers generate anchor charts to capture and celebrate increasing sophistication in oral language use." (p. 278)
If you substitute ‘understanding learning in mathematics’ for ‘oral language use,’ you have the purpose of this activity. (Follow a link for a free pdf of the first chapter, under samples.)
Create an Anchor Chart for Learning in Mathematics
1. Identify the concepts and ideas that you want to remember as they relate to doing mathematics.
2. Develop an anchor chart that captures and celebrates your increasing sophistication in understanding “Doing Mathematics.” This might be a list, or a mind map, or a representation of your own creation. You decide – just be prepared to share your chart during our next class.
3. Be sure you leave 10 minutes to reflect.
Reflection: How well does your group’s anchor chart capture what you want your future students to think of hen you ask them “what does it mean to do mathematics?”
Home Extension: You might want to check out how math teachers use anchor charts at books.google.com - Integrating Literacy and Math. by Ellen Fogelberg, Carole Skalinder, Patti Satz, Barbara Hiller, and Lisa Bernstein.
Other interesting examples:
(OK, the last one's mine.
Fair's fair if I'm putting up my students.
No, I don't know what's up with that guy's hair.)
Fair's fair if I'm putting up my students.
No, I don't know what's up with that guy's hair.)
Send me yours or your students' and I would be happy to post that!
Subscribe to:
Posts (Atom)