That's some of them...
By the way, if you haven't been following Megan Schmidt's spiral adventures, you're missing out.
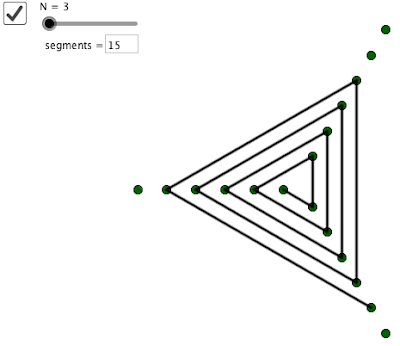
I've been interested in polygonal spirals for a while, but then my student Andrew's tessellation got me thinking again.
It's Archimedean since the spirals have a kind of constant width. At first I thought it was triangular, but it's clearly hexagonal. Interesting that two of them fit together to fill the space... that's something I need to think about more.
To build them in GeoGebra I made a list of N directional unit vectors, and then a scaling sum to get a spiral of points, like 1*v_1, 1*v_1+2*v_2, 1*v_1+2*v_2+3*v_3, ... with a modular function to reuse vectors in order.
Then I connected up to points 1/Nth of the way to corresponding vertices to make trapezoids. Then I rotated them N times, around a center I located by intersecting the perpendicular bisectors of points I wanted to correspond.
GeoGebra geek paragraph: The colors are the hardest thing to get, because in GeoGebra you can't set the color of different elements of a list. My current workaround was suggest by someone on the GeoGebra forums a few years ago, and I keep reworking it.
Execute[Sequence["Delete[R_{"+i+"}]", i, 1, oldN]]Essentially you constantly create and destroy objects from the elements in your list, and then set their color.
Execute[Sequence["Delete[R_{"+i+"}]", i, 1, oldN]]
SetValue[oldN,N]
Execute[Sequence["R_{"+i+"}=Element[list8, "+i+"]", i, 1, N]]
Execute[Sequence["SetDynamicColor[R_{"+i+"}, "+i/8+","+(.5+(i*(-1)^i)/(2*N))+","+1-i/8+",.75]", i, 1, N]]
Usually I have a list of color names and run through them with the SetColor, but in this one I wanted a higher opacity, so made up a way to set R, G and B values in the SetDynamicColor command.
Here's the result! It was hard to think about how else to dynamicize it, since it's a pretty rigid structure. Any ideas?
On GeoGebraTube, too.










No comments:
Post a Comment