Watched a nice video about Dor Abrahamson talking about how math is, or should be, about making sense.
In this video he describes a device to let students play with a proportion, and I thought it would be simple enough to do in GeoGebra, so... here you go! I'm pretty happy with the sketch, it's clean and the controls should be simple enough for young students. Close means within 5%, and Wow! is within 1%, so it's easier with a large unit. There's a lot of research supporting introducing fractions with a comparison model before the typical part-whole model, so it's nice to have a tool for that.
Available as a GeoGebra file or dynamic webpage. I've mostly stopped embedding GeoGebra files on the blog because it adds to load time significantly, it seems faster as a separate webpage.What other fraction representations would you like to see in a dynamic representation?
EDIT:
Made this before GeoGebraTube! I've updated this a little with a practice mode and more sensible checking. Here's the Teacher page (download) or the Student page (applet). Also have made this multiple choice fraction estimation applet.
Friday, September 30, 2011
Thursday, September 29, 2011
Patterning
I gave an algebra assessment this week (in SBG style) and a student really surprised me. So I thought I'd share.
The assessment:
Possibly relevant standards.
A. Algebra: representation, operations and modeling
 The problems: take 10 to 15 minutes to consider the following problems. You may do 1 a couple or all. Your SBG score will not depend on a correct answer, but rather on showing your understanding of the ideas involved. (Of course, good understanding helps find solutions, so it’s not totally unrelated; but it’s easy to give an answer and show no thinking.) Since the answers are not the central issue, be sure to communicate your thinking, process and understanding. If you read these instructions, clap your hands once.
The problems: take 10 to 15 minutes to consider the following problems. You may do 1 a couple or all. Your SBG score will not depend on a correct answer, but rather on showing your understanding of the ideas involved. (Of course, good understanding helps find solutions, so it’s not totally unrelated; but it’s easy to give an answer and show no thinking.) Since the answers are not the central issue, be sure to communicate your thinking, process and understanding. If you read these instructions, clap your hands once.
1. Using the parabolas at right, estimate the equations of the curves.
2. Discuss: how do you recognize a quadratic pattern from a table, and what does that have to do with the familiar parabola shape of the graph?
3. Use the idea of parallel and perpendicular slopes to give the coordinates for vertices of a square that has no sides parallel to an axis or to y=x. What is the area of your square?
4. Find a symbolic rule for one of the patterns below and look for connections between the symbolic and the visual. Extend the pattern one step to check your rule.


Analysis:
Problem 1 gives lots of nice information. Whether the student uses standard (harder) or vertex form, what the coefficients mean to them, and if they are consistent in applying that understanding amongst the different parabolas. Almost no one uses the roots, and I've yet to see someone apply regression to points.
Problem 2 pointed out that students over-identify parabolas with quadratics, as most students who struggled talked about increasing slope and symmetry as opposed to first or second differences. (Also that there was a homework that they didn't get to!)
Problem 3 was interesting in that no one started with the points. Everyone who tried it gave linear equations, established parallel and perpendicular, and struggled with how to get the sides to be equal length.
Problem 4 was the surprise. Most people chose the pattern on the left, and used visual identification of pieces to generate a direct rule. Only one student tried the pattern on the right. But instead of finding the quadratic pattern I intended, she noticed that each element was as long as the three previous elements summed. Definitely true for the picture... and got me to wondering if it would be quadratic. Nope. but definitely non-quadratic. I made a Google spreadsheet to compare, and this was unusual that the quadratic matched the sum of the first three pattern so well. I got interested in the ratios as they seemed to be converging. (Here's the spreadsheet if you want to play around for yourself.)
Finally I gave in, and looked up the sequence in the On-line Encyclopedia of Integer Sequences, where it is known as the tribonacci series. (Cute, eh?) This limit ratio is the solution of x^3 - x^2 - x - 1 = 0. I think I'll call it the Golden Ratio.
May your quizzes ever surprise you!
The assessment:
Possibly relevant standards.
A. Algebra: representation, operations and modeling
- Linear equations and functions
- Quadratic equations and functions
- Exponential and logarithmic equations and functions
- Higher polynomial and rational equations and functions
- Functional representation and operations.
 The problems: take 10 to 15 minutes to consider the following problems. You may do 1 a couple or all. Your SBG score will not depend on a correct answer, but rather on showing your understanding of the ideas involved. (Of course, good understanding helps find solutions, so it’s not totally unrelated; but it’s easy to give an answer and show no thinking.) Since the answers are not the central issue, be sure to communicate your thinking, process and understanding. If you read these instructions, clap your hands once.
The problems: take 10 to 15 minutes to consider the following problems. You may do 1 a couple or all. Your SBG score will not depend on a correct answer, but rather on showing your understanding of the ideas involved. (Of course, good understanding helps find solutions, so it’s not totally unrelated; but it’s easy to give an answer and show no thinking.) Since the answers are not the central issue, be sure to communicate your thinking, process and understanding. If you read these instructions, clap your hands once.1. Using the parabolas at right, estimate the equations of the curves.
2. Discuss: how do you recognize a quadratic pattern from a table, and what does that have to do with the familiar parabola shape of the graph?
3. Use the idea of parallel and perpendicular slopes to give the coordinates for vertices of a square that has no sides parallel to an axis or to y=x. What is the area of your square?
4. Find a symbolic rule for one of the patterns below and look for connections between the symbolic and the visual. Extend the pattern one step to check your rule.


Analysis:
Problem 1 gives lots of nice information. Whether the student uses standard (harder) or vertex form, what the coefficients mean to them, and if they are consistent in applying that understanding amongst the different parabolas. Almost no one uses the roots, and I've yet to see someone apply regression to points.
Problem 2 pointed out that students over-identify parabolas with quadratics, as most students who struggled talked about increasing slope and symmetry as opposed to first or second differences. (Also that there was a homework that they didn't get to!)
Problem 3 was interesting in that no one started with the points. Everyone who tried it gave linear equations, established parallel and perpendicular, and struggled with how to get the sides to be equal length.
Problem 4 was the surprise. Most people chose the pattern on the left, and used visual identification of pieces to generate a direct rule. Only one student tried the pattern on the right. But instead of finding the quadratic pattern I intended, she noticed that each element was as long as the three previous elements summed. Definitely true for the picture... and got me to wondering if it would be quadratic. Nope. but definitely non-quadratic. I made a Google spreadsheet to compare, and this was unusual that the quadratic matched the sum of the first three pattern so well. I got interested in the ratios as they seemed to be converging. (Here's the spreadsheet if you want to play around for yourself.)
Finally I gave in, and looked up the sequence in the On-line Encyclopedia of Integer Sequences, where it is known as the tribonacci series. (Cute, eh?) This limit ratio is the solution of x^3 - x^2 - x - 1 = 0. I think I'll call it the Golden Ratio.
May your quizzes ever surprise you!
Friday, September 23, 2011
Math(chat)misconceptions
I missed a good #mathchat last night. Chats are regularly scheduled twitter on-topic conversations. (Completish list; dizzying array of topics; mathchat is Thursday 8 pm (US-east) with a follow up on the same topic Monday at 3:30 pm.) You use twitters nice hashtag search feature to interact with people you may not typically follow (though it is a great place to find new follows). Mathchat, started by Colin Graham (@colintgraham), has a wiki page where topics are voted on and chats are archived. My current favorite way to follow is using TweetChat.
So if I missed the chat, how did I know it was a good one? There's the wiki archive, but also this time Bon Crowder (@mathfour) used Evernote to record and share the TweetChat record. Slick. It was good enough that I wanted to organize the list, which led me to figure to Tumbl it, but it turned into a blogpost when I realized the extent of the chat and that I had never blogged about mathchat before.
One thing that does not come across in this reorganized list is the conversational aspect. In Twitter you can click on a tweet and see all the previous tweets in that specific conversation.
People
Teaching
Field
Specific topics
Then what?
Photo credit: bfishshadow, petesimon @ Flickr
So if I missed the chat, how did I know it was a good one? There's the wiki archive, but also this time Bon Crowder (@mathfour) used Evernote to record and share the TweetChat record. Slick. It was good enough that I wanted to organize the list, which led me to figure to Tumbl it, but it turned into a blogpost when I realized the extent of the chat and that I had never blogged about mathchat before.
One thing that does not come across in this reorganized list is the conversational aspect. In Twitter you can click on a tweet and see all the previous tweets in that specific conversation.
People
- lostinrecursion must change misconception: you're either an applied person or a pure math person. Bleh
- mathheadinc Misconception: Students below 10th grade can't be in college algebra, calculus...
- daveinstpaul Misconception: People with "math brains" learn math effortlessly.
- LinaSouid misconception: Math teachers only know/care/love math.
- LinaSouid misconception: Girls aren't good at math. Girls don't make good engineers.
- lostinrecursion must change misconception: it's ok to say "I'm so dumb at math. I'm not just not a math person." especially for kids
- delta_dc misconception: "I'm not good at math." form many of my preservice elementary teachers.
- LinaSouid A majority of elem teachers at my school hated math. Spread it to all their students like a disease.
- daveinstpaul If I have to pick just one misconception, it has to be "I'm not good at math."
- MrHonner For me, this S misconception: "I'm good at math, so it's not important to work hard to become a better writer."
Teaching
- lostinrecursion must change misconception: math is math class and homework should look like homework
- lostinrecursion must change misconception: you really need to know algebra for the real world.
- lostinrecursion must change misconception: practice is the best way to get better. (personal experience actually is)
- LinaSouid #mathchat misconception: Math teachers know how to solve every problem, ever!
- lostinrecursion must change misconception: you have to play the role of "teacher" to get class to work.
- TenMarks Misconception: Memorization is the only way to learn math. (I'm looking at you, multiplication tables!)
- lostinrecursion must change misconception: "they" write the problems. I just answer them. Can we tell what "they're" asking?
- @lostinrecursion must change misconception: "there are problems I need to solve. I need someone to show me how to do that." - Salman Khan!
- @lostinrecursion #mathchat must realize: math is made by humans like the ones in the classroom. So let's make math.
- lostinrecursion must change misconception: stick to the book or you're in trouble (aka I don't trust you)
- delta_dc Many of the misconceptions in math are result of learners trying to make sense w/o understanding. @graceachen has 2 nice posts.
- LinaSouid misconception:" With a graphing calculator I can do anything"--especially from over confident high school students.
- lostinrecursion must change misconception: you need the teacher to learn math. You need school to learn math.
- lostinrecursion must change misconception: texting in class is bad. (I'm in field theory class enjoying this much more)
- rvdemerchant misconception: there is an old math and a new math.
- rvdemerchant old/new math? Did the old math think concept. understanding was bad? New math think procedural understanding bad? Nope
- delta_dc misconception: memorizing multiplication table will make one better at math. A lot of parents of MS kids say this.
- MrHonner I think the primary teaching misconception is "There is 1 right way to solve this problem."
- cheesemonkeysf IMHO this is also the primary TESTING misconception!
- MrHonner It is related to this misconception: "It is wrong for the teacher to admit they don't know something".
- LinaSouid I don't know when math teachers (20 years ago) learned that part of their job was to be socially inept
- mathheadinc Probably when they themselves were humiliated, probably at an early age. Vicious cycle
Field
- ColinTGraham For me, if it was only one chance... I would want to change the idea that mathematics is about doing calculations.
- MariaDroujkova Clear one misconceptions! math=arithmetic
- ekendriss Misconception I'd like to clear: Statistics = boring.
- MrHonner Major Math Misconception: There's only one right way to solve this problem. ColinTGraham Or: there *is* a right way....
- msnorthrup Luckily this is fading with elem tchrs RT @MrHonner the primary tchg misconception is "There's one right way to solve a problem"
- MrHonner Misconception: The most important thing is math is whether your answer is right or wrong
- MrHonner Student Misconception: "If I try something and it didn't work, I've done something wrong."
- shawn_ny That it lacks creativity.
- delta_dc Misconception - being fast at math means being good at math.
- LinaSouid misconception: You need to know how to prove something to use it and understand it.
- LinaSouid: misconception: You can't guess.
- lostinrecursion must change misconception: go with your first instinct. Your second is wrong (aka don't trust yourself)
- delta_dc Misconception - math is only worthwhile if it applies to real world.
- OoeyGooeyLady That u can "like" it but still struggle at it. I didn't need it 2 be easy. Just wanted to have chance to try!!
- LinaSouid So true. People focus on perfection. Another misconception!
Specific topics
- daveinstpaul Misconceptions: y is always a function of x. 0^0 cannot be consistently defined. √4 has two values. Everyone should take algebra.
- daveinstpaul 4 has two square roots, which are denoted √4 and -√4. By itself √4 indicates the positive square root.
- ColinTGraham By convention = accepted academic 'whatever'
- lostinrecursion must change misconception: fractions are wrong if they're not reduced.
- mathheadinc Misconception: This is not how to write a fraction (1 1/2)/4
- daveinstpaul Oh, another misconception: All polygons are convex.
- MathMatters2Me Misconception: radicals can never be left in the denominator
- MathMatters2Me Misconception: Asymptotes are lines a graph approaches but never touches
- MrHonner For purely math misconceptions, nothing beats sqrt(a^2 + b^2) = a + b.
- msnorthrup As a 5th grade teacher - the misconception that "You can't take a big number from a small number" is rampant and problematic
- daveinstpaul Misconception: When proving a trigonometric identity, you must work with one side of the equation at a time.
- MrCHRISatCSI You don't have to carry a one!
 |
| Is Google cooking the books? |
Then what?
- LinaSouid Misconceptions will be resolved when math teachers are friendly, social, good role models
- ColinTGraham "friendly, social, good role models" depends very much on how people arrive at teaching mathematics...
- MariaDroujkova I am making a poster of today's #mathchat about misconceptions. So much concentrated math ed genius! You rock, #mathchat people!
- MrHonner We need to remind ALL teachers that they teach kids, not math.
Photo credit: bfishshadow, petesimon @ Flickr
Saturday, September 3, 2011
Pattern Generators
I like the theme of the first week of my Math for High School course to be teaching for creativity.
This semester's group did a nice job with Dan Meyer's Toast video. I had them ask questions and record what they noticed. There was a neat dichotomy: the WCYDWT responses were all pretty traditional math textbook questions. The what they noticed branched far afield, wondering what would make a good soundtrack, wondering about darkness of toast and toaster design.
We followed that with a workshop (I think based on an Esther Billings and Pam Wells workshop) based on verbalizing and algebrafying number patterns.
The last workshop of the day was planned to be this, which in the past has been a pretty good activity:
So what we did was:
I'm kicking myself now that I didn't take more pictures. Most students made repeating linear patterns, some tessellation patterns, one person made a circular pattern, and then there was...
This was the only pattern that students did not see as a pattern. It was described as just random fitting together, and someone asked about the yellow. "They were supposed to be orange." And then the author shared how they were lines of blocks fit together. Another student shared how to her it was a skewed checkerboard. Then the class unanimously agreed it was a pattern. I thought that was really interesting and asked how they would verbalize it. Good descriptions followed. Could they capture it symbolically? No, not that I expected it. So I shared a bit about the wallpaper groups, and how mathematicians seek the power of good notation so they can symbolically manipulate. I also shared how I had thought the yellow was a pattern in a pattern.
The characteristics of patterns they thought most important was that it can be explained (there is an idea or structure) and someone who understands it can extend it or fill in a missing piece.
If one week determines a pattern, it's going to be a good semester!
Photo credit: The tremendous image up top is from Tanya Khovanova, in this post. The original question was rather brilliant: "Which one of these things does not belong?" Many thanks to Sue, who pointed out the author below.
This semester's group did a nice job with Dan Meyer's Toast video. I had them ask questions and record what they noticed. There was a neat dichotomy: the WCYDWT responses were all pretty traditional math textbook questions. The what they noticed branched far afield, wondering what would make a good soundtrack, wondering about darkness of toast and toaster design.
We followed that with a workshop (I think based on an Esther Billings and Pam Wells workshop) based on verbalizing and algebrafying number patterns.
 |
| Is this a pattern? |
The last workshop of the day was planned to be this, which in the past has been a pretty good activity:
Objective: TLW develop mathematical patterns from the teacher’s perspective.But we didn't have time for that! (Not to butter them up, but they were jamming on the toast and I didn't want to cut that short.)
Schema Activation: when (if you do) do you notice patterns in real life?
Focus: What we talked about in Class 01 was really curriculum. What are we going to teach? Here’s the NCTM’s take:
The Curriculum Principle
A curriculum is more than a collection of activities: it must be coherent, focused on important mathematics, and well articulated across the grades. A school mathematics curriculum is a strong determinant of what students have an opportunity to learn and what they do learn. In a coherent curriculum, mathematical ideas are linked to and build on one another so that students' understanding and knowledge deepens and their ability to apply mathematics expands. An effective mathematics curriculum focuses on important mathematics—mathematics that will prepare students for continued study and for solving problems in a variety of school, home, and work settings. A well-articulated curriculum challenges students to learn increasingly more sophisticated mathematical ideas as they continue their studies. (From the Principles and Standards for School Mathematics (PSSM for short), NCTM. All these principles have expanded information and explanation at the NCTM website.)
As we discussed, there are small shifts and large shifts. This activity applies to both: it’s an easy activity that allows for creativity (subtle shift) but may lead to you designing your own problems and questions for students (big shift).
Activity: we have blocks. Play with them!
1. Make a pattern of images with the blocks. A successful pattern for this task is one in which the next shape is determined, or is reasonable.
2. Describe your pattern in words. What’s happening, what’s changing? What can you say about the next step compared to the previous? What will the 10th step be like? A general step?
3. Describe your pattern mathematically. What can you say about the next step compared to the previous? What will the 10th step be like? The Nth step?
4. What connections do you see amongst 1 (the visual), 2 (the verbal), and 3 (the symbolic or mathematical)?
5. Repeat as time allows.
Reflection: choose 2
• Was this task too open-ended? Does it need more structure?
• Was this task engaging? Was it mathematically worthwhile?
• What were the strongest or most interesting connections you saw in a step 4?
So what we did was:
Schema Activation: whole class discussion - what makes a pattern a pattern?
Focus: Pattern blocks, make what you consider a pattern.
Activity:
1. Make patterns.
2. Put a piece of scrap paper by your pattern with a Y and an N.
3. Gallery walk. Put a hashmark by yes or no if you consider that a pattern or not.
4. Stop by someone else's pattern, add three blocks.
Reflection: whole class discussion about what happened.Record your personal definition of pattern as it is now.
I'm kicking myself now that I didn't take more pictures. Most students made repeating linear patterns, some tessellation patterns, one person made a circular pattern, and then there was...
This was the only pattern that students did not see as a pattern. It was described as just random fitting together, and someone asked about the yellow. "They were supposed to be orange." And then the author shared how they were lines of blocks fit together. Another student shared how to her it was a skewed checkerboard. Then the class unanimously agreed it was a pattern. I thought that was really interesting and asked how they would verbalize it. Good descriptions followed. Could they capture it symbolically? No, not that I expected it. So I shared a bit about the wallpaper groups, and how mathematicians seek the power of good notation so they can symbolically manipulate. I also shared how I had thought the yellow was a pattern in a pattern.
The characteristics of patterns they thought most important was that it can be explained (there is an idea or structure) and someone who understands it can extend it or fill in a missing piece.
If one week determines a pattern, it's going to be a good semester!
Photo credit: The tremendous image up top is from Tanya Khovanova, in this post. The original question was rather brilliant: "Which one of these things does not belong?" Many thanks to Sue, who pointed out the author below.
Friday, September 2, 2011
Bamboo and Mac
 |
| x-a-v-i.blogspot.com |
Why not Google? There was a Neil Gaiman quote I saw recently: "Google can bring you back 100,000 answers, a librarian can bring you the right one." Well, Twitter is like a few hundred librarians.
So far I've used Jarnal for writing on paper, and the Corel Painter Essentials that came with the board for more serious stuff. (Like my friend's Juvenile Diabetes Research Foundation team logo.) The Corel can import images but that would be slooow and big to save. Apple's native Preview has annotation tools, but nothing freehand. No support for math typing. Nice tool suite though, with stickies, side notes, highlighting and direct typing. The edits are visible in other programs that you can use to read pdfs.
Twitter says...
@scsocha named Adobe Pro. Obviously great if you have access, which I don't think we do...
I didn't realize Jarnal was a PDF annotator as well, until @bennettscience replied about it. Before getting the pdf, set your paper (Format > Paper and Background) to plain white. (You can do it afterwords, but Jarnal works page by page so...) You can have multiple windows open at a time... flexible and nice. Playing more with it made me realize that I am not using this program enough. It is a Java application, so it lacks some of the feel of a native Mac program. But it runs multiplatform.
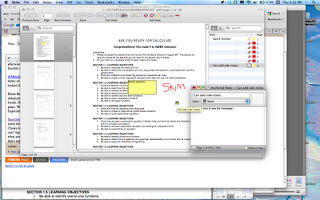
@MitchKeller recommended Skim. It has great features, including stickies like Adobe Pro. A nice index of annotations. But the notes were only visible in Skim. When I opened in any other program it looked like the original. That doesn't make a lot of sense to me, so I'm probably missing something. Other than that, the functionality made it Preview Plus, which is a pretty good recommendation.
EDIT: Mitch gives advice in the comments about how he correctly uses Skim for this. "you do have to be sure to export the file as PDF with Embedded Notes and not just save it." Makes sense.
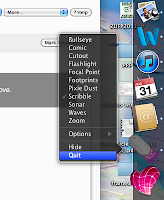
Brian Bennett also suggested Omnidazzle, which was entirely new to me. Turns out that it is a cursor enhancement program, enabling you to do funky stuff with your cursor, like spread pixie dust or sonar locate. However it also enables you to turn your cursor into a pen to write on screen and a magnifying glass. Won't help for this job, but seems useful for online teaching when you're showing your desktop. Especially the magnifier since Macs can't use the one that all my PC colleagues use.
 |
| OmniDazzle - Magnify mode |
 |
| OmniDazzle - Cutout mode |
Sketchbook Express was suggested by @kellyoshea. At first I couldn't get this to download - I got some kind of error about 'not available in US.' Finally opened in App Store (maybe it was trying to use iTunes before?) Good enough for drawing to make me think about the Sketchbook Pro for $60. But... I can't figure out how to open pdfs directly. Undoubtedly you could convert in preview, or screen capture what you want to comment on with Jing or the native ⌘-shift-4 (⌘-shift-3 for the whole desktop), but that's not suitable for heavy use.
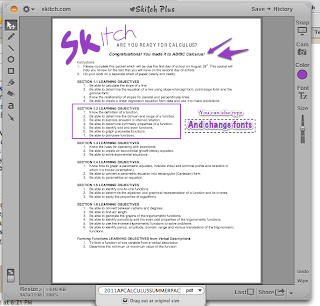 Skitch was the last program I checked out; just bought by Evernote, so it works well on mobile devices, too. This is kind of like Jing+ on pictures, - Jing's video features. Definitely the best free screencap program I've used. It has already earned a regular spot in the starting rotation for me. Skitch has an online sharing feature (like Jing/Evernote) or can email directly the image you're making. It can open common image formats, including pdfs, but just shows you the first page. It can export to pdf, even starting as a screencap, though. The easy sharing options might make it worth using for student feedback, though. Skitch runs from the menu bar, which is a nice feature.
Skitch was the last program I checked out; just bought by Evernote, so it works well on mobile devices, too. This is kind of like Jing+ on pictures, - Jing's video features. Definitely the best free screencap program I've used. It has already earned a regular spot in the starting rotation for me. Skitch has an online sharing feature (like Jing/Evernote) or can email directly the image you're making. It can open common image formats, including pdfs, but just shows you the first page. It can export to pdf, even starting as a screencap, though. The easy sharing options might make it worth using for student feedback, though. Skitch runs from the menu bar, which is a nice feature.This has been fun. I'll definitely play more with Jarnal and Skitch, and test out Sketchbook Express to replace Corel Painter Essentials.
What do you use?
Subscribe to:
Posts (Atom)











